mcsm-benchs: Benchmarks with personalized noise-generating functions

import numpy as np
from numpy import pi as pi
import pandas as pd
import scipy.signal as sg
from matplotlib import pyplot as plt
from mcsm_benchs.Benchmark import Benchmark
from mcsm_benchs.ResultsInterpreter import ResultsInterpreter
from utils import spectrogram_thresholding, get_stft

Creating a dummy dictionary of methods

First let us define a dummy method for testing. Methods should receive a numpy array with shape (N,) where N is the number of time samples of the signal. Additionally, they can receive any number of positional or keyword arguments to allow testing different combinations of input parameters. The shape of the output depends on the task (signal denoising or detection). So the recommended signature of a method should be the following:

output = a_method(noisy_signal, *args, **kwargs).

If one set task='denoising', output shoud be a (N,) numpy array, i.e. the same shape as the input parameter noisy_signal, whereas if task='detection', the output should be boolean (0 or False for no signal, and 1 or True otherwise).

After this, we need to create a dictionary of methods to pass the Benchmark object at the moment of instantiation.

def method_1(noisy_signal, *args, **kwargs):
    # If additional input parameters are needed, they can be passed in a tuple using
    # *args or **kwargs and then parsed.
    xr = spectrogram_thresholding(noisy_signal,1.0,fun='hard')
    return xr

def method_2(noisy_signal, *args, **kwargs):
    # If additional input parameters are needed, they can be passed in a tuple using
    # *args or **kwargs and then parsed.
    xr = spectrogram_thresholding(noisy_signal,2.0,fun='soft')
    return xr

# Create a dictionary of the methods to test.
my_methods = {
    'Method 1': method_1,
    'Method 2': method_2,
    }

Benchmarks with different kinds of noise

Now we are ready to instantiate a Benchmark object and run a benchmark using the proposed methods.

The Benchmark constructor receives a number of input parameters. The parameter complex_noise can be True or False indicating if the simulations are to be done using white complex Gaussian noise or not. However, if a function is passed instead of a bool variable, the function is called in order to obtain a different realization of noise. The noise generator function must receive an int variable indicating the length of the time series to generate: noise = noise_generator_fun(N,).

Real White Gaussian noise (default)

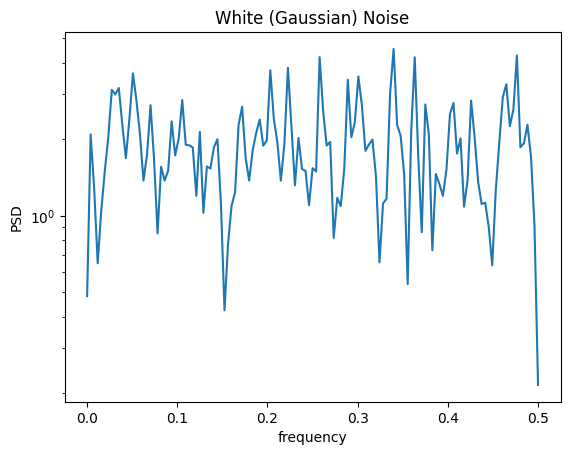
# Benchmark class uses np.random.randn(N,) to generate noise realizations
n = np.random.randn(1024)

f, Pxx_den = sg.welch(n)
plt.semilogy(f, Pxx_den)
plt.xlabel('frequency')
plt.ylabel('PSD')
plt.title('White (Gaussian) Noise')
plt.show()

benchmark = Benchmark(task = 'denoising', # defines the default performance function
                        methods = my_methods, # dictionary of methods
                        N = 256,  # Length of the signals
                        SNRin = [40, 50], # SNRs to use during the test
                        repetitions = 3, # Number of noise realizations to use
                        signal_ids=['LinearChirp', 'CosChirp',], # Signals to use
                        complex_noise=False # Real white Gaussian Noise
                        )

benchmark.run() # Run the test.
results_df = benchmark.get_results_as_df() # This formats the results on a DataFrame
results_df

Running benchmark...
- Signal LinearChirp

  0%|          | 0/2 [00:00<?, ?it/s]100%|██████████| 2/2 [00:00<00:00, 418.51it/s]

- Signal CosChirp

100%|██████████| 2/2 [00:00<00:00, 354.07it/s]

The test has finished.

	Method	Parameter	Signal_id	Repetition	40	50
6	Method 1	((), {})	CosChirp	0	35.810596	35.848604
7	Method 1	((), {})	CosChirp	1	35.076937	36.675817
8	Method 1	((), {})	CosChirp	2	34.878397	35.250035
0	Method 1	((), {})	LinearChirp	0	40.716980	45.830269
1	Method 1	((), {})	LinearChirp	1	40.761751	44.879363
2	Method 1	((), {})	LinearChirp	2	40.506275	44.715266
9	Method 2	((), {})	CosChirp	0	22.325833	21.801351
10	Method 2	((), {})	CosChirp	1	20.850857	21.708549
11	Method 2	((), {})	CosChirp	2	21.080309	21.317084
3	Method 2	((), {})	LinearChirp	0	35.733726	37.497704
4	Method 2	((), {})	LinearChirp	1	35.193784	36.680307
5	Method 2	((), {})	LinearChirp	2	36.448123	37.518342

Pink noise

Let’s first import a function to generate colored noise, and later pass it as a parameter to the Benchmark class constructor.

from utils import voss

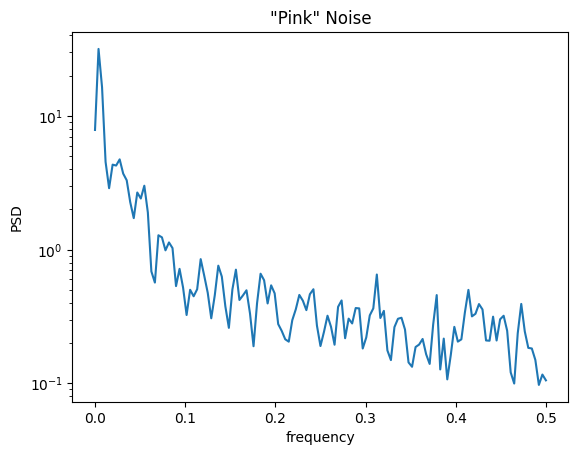
#Generates pink noise using the Voss-McCartney algorithm.
noise_fun = lambda N : voss(N,)
n = noise_fun(1024)

f, Pxx_den = sg.welch(n)
plt.semilogy(f, Pxx_den)
plt.xlabel('frequency')
plt.ylabel('PSD')
plt.title('"Pink" Noise')
plt.show()

benchmark = Benchmark(task = 'denoising', # defines the default performance function
                        methods = my_methods, # dictionary of methods
                        N = 256,  # Length of the signals
                        SNRin = [40, 50], # SNRs to use during the test
                        repetitions = 3, # Number of noise realizations to use
                        signal_ids=['LinearChirp', 'CosChirp',], # Signals to use
                        complex_noise=noise_fun, # "Pink" Noise
                        verbosity=0,
                        )

benchmark.run() # Run the test.
results_df = benchmark.get_results_as_df() # This formats the results on a DataFrame
results_df

Running benchmark...

100%|██████████| 2/2 [00:00<00:00, 326.96it/s]
100%|██████████| 2/2 [00:00<00:00, 187.86it/s]

	Method	Parameter	Signal_id	Repetition	40	50
6	Method 1	((), {})	CosChirp	0	35.191254	35.957057
7	Method 1	((), {})	CosChirp	1	35.210970	35.960973
8	Method 1	((), {})	CosChirp	2	36.105207	36.592537
0	Method 1	((), {})	LinearChirp	0	40.903732	46.124983
1	Method 1	((), {})	LinearChirp	1	41.337536	46.151734
2	Method 1	((), {})	LinearChirp	2	40.517168	45.670656
9	Method 2	((), {})	CosChirp	0	21.463604	21.583236
10	Method 2	((), {})	CosChirp	1	21.182747	21.645561
11	Method 2	((), {})	CosChirp	2	21.755696	21.611189
3	Method 2	((), {})	LinearChirp	0	34.107279	37.318161
4	Method 2	((), {})	LinearChirp	1	35.669359	37.793854
5	Method 2	((), {})	LinearChirp	2	35.873981	37.461903